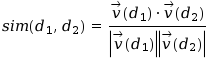Scoring and Ranking Techniques - tf-idf term weighting and cosine similarity
Published Mar 31, 2010 by Michael Dittenbach
What mechanisms determine which documents are retrieved and how is the relevance score calculated that finally determines the ranking?
Scoring and Ranking Techniques: tf-idf Term Weighting and Cosine Similarity
Quite a number of different full-text search technologies are being developed by academic and non-academic communities and made available as open source software. On the engineering side, one obvious set of differentiators are technological features like connectors to data sources, support for indexing various document formats, ability to run distributed on multiple servers, incremental indexing and the like. But in the end, what users see is a ranked list of - hopefully relevant - documents.
In the typical Web search setting it is important to users that the most relevant documents are top-ranked given the large number of potentially relevant documents. In the area of professional search where users usually spend comparatively more time on investigating a larger portion of the search result than the casual Web searcher, information professionals also benefit from finding relevant information earlier when working through potentially long result list.
What actually leads to a particular ranking of search results is influenced by a multitude of factors: What are the basic units (tokens) that represent the documents (tokenization, preprocessing like stopword removal or stemming)? How do you assign weights marking the importance of these tokens for the documents? What mechanisms determine which documents are retrieved and how is the relevance score calculated that finally determines the ranking?
In this article, which will be the start of a series of articles about ranked retrieval, we concentrate on the latter two and introduce tf-idf term weighting, the vector space model and the cosine similarity measure for relevance score calculation. Please note that for the sake of simplicity and to avoid linguistic nit-picking the notions of token, term and word are used interchangeably in this article. A token in an index could actually be a multi-word term.
Tf-idf term weighting
In contrast to plain Boolean retrieval where -in principle - only the presence of terms in documents needs to be recorded in the index, a term can also be assigned a weight that expresses its importance for a particular document. A commonly used term weighting method is tf-idf, which assigns a high weight to a term, if it occurs frequently in the document but rarely in the whole document collection. Contrarily, a term that occurs in nearly all documents has hardly any discriminative power and is given a low weight, which is usually true for stopwords like determiners, but also for collection-specific terms; think of apparatus, method or claim in a corpus of patent documents. For calculating the tf-idf weight of a term in a particular document, it is necessary to know two things: how often does it occur in the document (term frequency = tf), and in how many documents of the collection does it appear (document frequency = df). Take the inverse of the document frequency (= idf) and you have both components to calculate the weight by multiplying tf by idf. In practice, the inverse document frequency is calculated as the logarithm (base 10) of the quotient of the total number of documents (N) and the document frequency in order to scale the values.
In literature, various incarnations of the tf-idf formula exist, which try to better model the significance of terms in documents (for examples see pp. 126-132, Manning et al., 2008).
Vector space model
The tf-idf values can now be used to create vector representations of documents. Each component of a vector corresponds to the tf-idf value of a particular term in the corpus dictionary. Dictionary terms that do not occur in a document are weighted zero. Using this kind of representation in a common vector space is called vector space model (Salton et al., 1975), which is not only used in information retrieval but also in a variety of other research fields like machine learning (e.g. clustering, classification). Each dimension of the space - we are far beyond 3D when it comes to text - corresponds to a term in the dictionary. Remembering what we learned in trigonometry lessons at school, a vector space provides the possibility to perform calculations like computing differences or angles between vectors. Since documents are usually not of equal length, simply computing the difference between two vectors has the disadvantage that documents of similar content but different length are not regarded as similar in the vector space.
Cosine similarity measure
To avoid the bias caused by different document lengths, a common way to compute the similarity of two documents is using the cosine similarity measure. The inner product of the two vectors (sum of the pairwise multiplied elements) is divided by the product of their vector lengths. This has the effect that the vectors are normalized to unit length and only the angle, more precisely the cosine of the angle, between the vectors accounts for their similarity.
Documents not sharing a single word get assigned a similarity value of zero because of the orthogonality of their vectors while documents sharing a similar vocabulary get higher values (up to one in the case of identical documents). Because a query can be considered a short document, it is of course possible to create a vector for the query, which can then be used to calculate the cosine similarities between the query vector and those of the matching documents. Finally, the similarity values between query and the retrieved documents are used to rank the results.
An Example
Consider the data in the following table as an example of term and document frequencies for four terms in three documents of a fictional collection consisting of 1,000 documents. It can be seen that the inverse document frequency for a stopword appearing in all documents is zero and for a term like "method" which is quite likely to appear in patents, for example, the idf is rather low. A very specific term like "bioreactor", which appears in only 25 of 1,000 documents, gets assigned a comparatively high idf.
term tf(doc1) tf(doc2) tf(doc3) df idf
method 4,250 3,400 5,100 850 0.07
the 50,000 43,000 55,000 1,000 0.00
water 7,600 4,000 2,000 400 0.40
bioreactor 600 0 25 25 1.6
The tf-idf values are as follows:
term tf-idf(doc1) tf-idf(doc2) tf-idf(doc3)
method 299.97 239.98 359,96
the 0.00 0.00 0.00
water 3,024.34 1,591.76 795.88
bioreactor 961.24 0.00 40.05
Here it can be seen how the inverse document frequency influences the tf-idf value. Even though the term "method" occurs nearly as often as "water" in document doc2, the tf-idf value of "water" is roughly 6.6 times higher.
Finally, a query consisting of the two terms "method" and "bioreactor" would assign document doc1 a score of 0.15 and doc3 a score of 0.04.
References
G. Salton, A. Wong, and C. S. Yang (1975), A Vector Space Model for Automatic Indexing, Communications of the ACM, vol. 18, nr. 11, pp. 613-620.
C. D. Manning, P. Raghavan and H. Schütze (2008), Introduction to Information Retrieval, Cambridge University Press.